A L-System is a formal grammar with :
- An alphabet V : The set of the variables of the L-System. V * stands for the set of the “words” we
could generate with any symbols taken from alphabet V , and V + the set of “words” with at least one
symbol.
- A set of constant values S. Some of this symbol are common to all L-System. (in particular with the
turtle!).
- A start awiom ω taken from V + , it is the initial state.
- A set of prodution rules P of the V symbols.
Such a L-System is defined as a tuple {V,S,ω,P}.
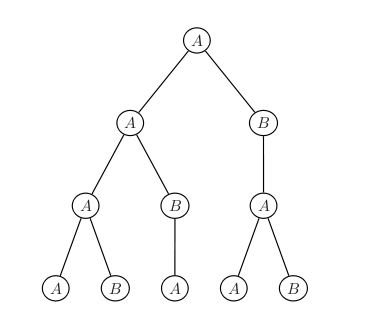
Let’s consider the following L-system:
- Alphabet : V = {A,B}
- Constants : S = {∅}
- Start Axiom: ω = A
- Rules :
The two production rules are rewriting rules. On each step, the symbol A is replaced by the séequence AB, and the
symbol B is replaced by A. Here are the first iterations of this Lindemayer system:
- Itération 1: A
- Itération 2: AB
- Itération 3: ABA
- Itération 4: ABAAB
Ok, ok but concretely? Let’s read next section!