The main advantage of the previous program is to exploit the recursive structure of the solid. This method is quite
similar to the one we used to draw the Van Koch snowflake on p.. The main advantage of using recursion
is a quite natural short program code. The disadvantage of the recursive approach is the number of
created polygons: for example, a sponge of order 3 needs 48 000 polygons. XLOGO requires in this
case an internal memory set to 256 Mb in the Preferences panel to prevent from memory overflow.
If we want to draw a Menger sponge, order 4, we have to rethink the program and to forget recursion.
We’re going to create in this section a program that will draw the Menger solid of order 0,1,2,3 or
4.
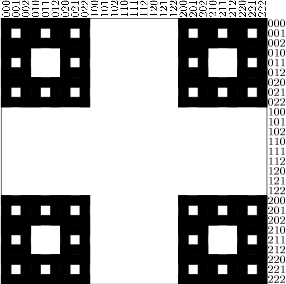
Menger’s sponge is the generalization in 3 dimensions of a plane figure called “the Sierpinski carpet”. Here are the
first steps to generate this figure:

Step 0

Step 1

Step 2

Step 3
Each face of a Menger sponge of order p is a Sierpinski carpet of order p.
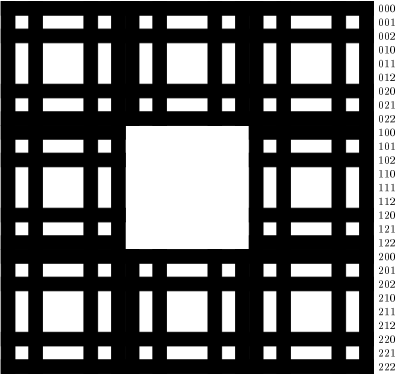
The objective is to set minimal the number of polygon to draw a Sierpinski carpet. The following example explains
how to draw a Sierpinski carpet of order 3. Here, the first square has 33 = 27 lines and 27 columns. We write in
3-basis each line number and each column number.
- First step: For each line whose number doesn’t contain any 1, we draw a 27 units line. Using symmetry, we
repeat the same operation on columns.
- Second step: Now, we’re looking at lines whose numbers have a single 1 in first place. We draw rectangles of
9 units length by alternation.
- Third step: Now we’re looking at lines whose number contains a single 1 in second place. We draw rectangles
following the schema [3 3 6 3 6 3 3]. (It means 3 units pen down, 3 units pen up, 6 units pen down etc...).
Using symmetry, we repeat this operation on columns.
- Final step: Now we’re looking at lines whose number contains a double 1 in the first two positions. We
draw rectangles alternating following the schema [3 3 3 9 3 3 3]. We repeat this operation on
columns.
Now, we have built a Sierpnski carpet of order 3. To draw such a carpet, we need: 16 + 16 + 32 + 16 = 80
polygons.
To recapitulate, here are the different column schemas according to the line numbers. (The symbol * represents 0 or
2)
|
|
| Number of line | Schema to apply |
|
|
| *** | 27 |
|
|
| 1** | 9 9 9 |
|
|
| *1* | 3 3 6 3 6 3 3 |
|
|
| 11* | 3 3 3 9 3 3 3 |
|
|
| |
In the same way, to build a carpet of order 4, we need a square with 34 = 81 units. The line and column numbers will
have 4 numbers in their writing in 3-basis. For each line number, here is the schema to apply (the symbol *
represents 0 or 2):
|
|
| Line number | Schema to apply |
|
|
| **** | 81 |
|
|
| 1*** | 27 27 27 |
|
|
| *1** | 9 9 18 9 18 9 9 |
|
|
| **1* | 3 3 6 3 6 3 6 3 6 3 6 3 6 3 6 3 6 3 3 |
|
|
| *11* | 3 3 3 9 3 3 6 3 3 9 3 3 6 3 3 9 3 3 3 |
|
|
| 1*1* | 3 3 6 3 6 3 3 27 3 3 6 3 6 3 3 |
|
|
| 11** | 9 9 9 27 9 9 9 |
|
|
| 111* | 3 3 3 9 3 3 3 27 3 3 3 9 3 3 3 |
|
|
| |
496 polygons are necessary to draw the a Sierpinski carpet of order 4.
Finally, here are the schema to apply for solid of order 2:
|
|
| Line numbers | Schema to apply |
|
|
| ** | 9 |
|
|
| 1* | 3 3 3 |
|
|
| |
# Draws a Sierpinski carpet of order :p and size :size
to carpet :size :p
globalmake "unit :size/(power 3 :p)
if :p=0 [ rec :size :size stop]
if :p=1 [repeat 4 [rec :size :unit forward :size right 90 ] stop]
for (list "x 1 power 3 :p) [
localmake "cantorx cantor :x :p []
# We didn’t draw elements with a 1 in last position
if not (1=last :cantorx) [
localmake "nom evalue butlast :cantorx "
drawcolumn :x getproperty "map :nom
]
]
end
# output the writing in 3-basis of number x
# p order of the carpet (3^p units)
# :list empty list
to cantor :x :p :list
if :p=0 [output :list]
localmake "a power 3 :p-1
if :x<= :a [
output cantor :x :p-1 sentence :list 0]
[ if :x<=2*:a [output cantor :x-:a :p-1 sentence :list 1]
output cantor :x-2*:a :p-1 sentence :list 0]
end
# Draw the column number x respecting the schema in list :list
to drawcolumn :x :list
penup right 90 forward (:x-1)*:unit left 90 pendown des :list
penup left 90 forward (:x-1)*:unit right 90 forward :x*:unit right 90 pendown des :list
penup left 90 back :x*:unit pendown
end
# Draws a rectangle with choosen dimensions
# It is stored in 3D viewer
to rec :lo :la
globalmake "compteur :compteur+1
polystart
repeat 2 [forward :lo right 90 forward :la right 90]
polyend
end
# Inits the different possible columns for carpet order 0 to 4
to initmap
putproperty "map 111 [3 3 3 9 3 3 3 27 3 3 3 9 3 3 3]
putproperty "map 110 [9 9 9 27 9 9 9]
putproperty "map 101 [3 3 6 3 6 3 3 27 3 3 6 3 6 3 3]
putproperty "map 011 [3 3 3 9 3 3 6 3 3 9 3 3 6 3 3 9 3 3 3]
putproperty "map 000 [81]
putproperty "map 100 [27 27 27]
putproperty "map 010 [9 9 18 9 18 9 9]
putproperty "map 001 [3 3 6 3 6 3 6 3 6 3 6 3 6 3 6 3 6 3 3]
putproperty "map 01 [3 3 6 3 6 3 3]
putproperty "map 00 [27]
putproperty "map 10 [9 9 9]
putproperty "map 11 [3 3 3 9 3 3 3]
putproperty "map 1 [3 3 3]
putproperty "map 0 [9]
end
# if the 3-basis writing is [1 0 1] --> output 101
to evalue :list :mot
if emptyp :list [output :mot]
[
localmake "mot word :mot first :list
output evalue butfirst :list :mot
]
end
# Draws the block of rectangles alternanting
to des :list
localmake "somme 0
for (list "i 1 count :list) [
localmake "element item :i :list
localmake "somme :element+:somme
if even? :i [penup forward :element*:unit pendown ] [rec :element*:unit :unit forward :element*:unit]
]
penup back :somme * :unit pendown
end
# Is this number even?
to pair? :i
output 0=reste :i 2
end
# Draws the carpet order :p
to tapis :p
clearscreen 3d hideturtle initmap
globalmake "compteur 0
carpet 810 :p
write "nombre\ de\ polygones:\ print :compteur
view3d
end
# Is this number even?
to even? :i
output 0=modulo :i 2
end
tapis 3 draws a Sierpinski carpet of order 3 with a side length equal to 810. Here we are! Now we can come back
to the Menger’s sponge!
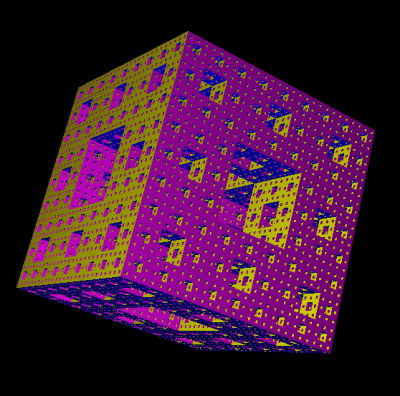
The Menger sponge has a lot of symmetries. To build the sponge, we’re going to draw the different sections along
the plane (xOy) and then repeat those figures along the planes (yOz) and (xOz). To explain what happens, let’s
have a look at the sponge of order 2:
When we cut with a vertical plane, we can obtain four different motifs:
To draw a sponge of order 3, we’re going to browse the number from 1 to 27, it means from 001 to 222 in 3
basis. For each number, we’ll apply the valid section and we’ll report this figure along (Ox), (Oy) and
(Oz).
With this program, we can draw Menger’s sponge of order 0,1,2,3 and 4.
# Draws a Sierpinski carpet of order :p and size :size
to carpet :size :p
globalmake "unit :size/(power 3 :p)
if :p=0 [ rec :size :size stop]
if :p=1 [repeat 4 [rec :size :unit forward :size right 90 ] stop]
for (list "x 1 power 3 :p) [
localmake "cantorx cantor :x :p []
# We didn’t draw elements with a 1 in last position
if not (1=last :cantorx) [
localmake "nom evalue butlast :cantorx "
drawcolumn :x getproperty "map :nom
]
]
end
# output the writing in 3-basis of number x
# p order of the carpet (3^p units)
# :list empty list
to cantor :x :p :list
if :p=0 [output :list]
localmake "a power 3 :p-1
if :x<= :a [
output cantor :x :p-1 sentence :list 0]
[ if :x<=2*:a [output cantor :x-:a :p-1 sentence :list 1]
output cantor :x-2*:a :p-1 sentence :list 2]
end
# Draw the column number x respecting the schema in list :list
to drawcolumn :x :list
penup right 90 forward (:x-1)*:unit left 90 pendown des :list
penup left 90 forward (:x-1)*:unit right 90 forward :x*:unit right 90 pendown des :list
penup left 90 back :x*:unit pendown
end
# Draws a rectange with choosen dimensions
# It is stored in 3D viewer
to rec :lo :la
globalmake "counter :counter+1
polystart
repeat 2 [forward :lo right 90 forward :la right 90]
polyend
end
# Inits the different possible columns for carpet order 0 to 4
to initmap
putproperty "map 111 [3 3 3 9 3 3 3 27 3 3 3 9 3 3 3]
putproperty "map 110 [9 9 9 27 9 9 9]
putproperty "map 101 [3 3 6 3 6 3 3 27 3 3 6 3 6 3 3]
putproperty "map 011 [3 3 3 9 3 3 6 3 3 9 3 3 6 3 3 9 3 3 3]
putproperty "map 000 [81]
putproperty "map 100 [27 27 27]
putproperty "map 010 [9 9 18 9 18 9 9]
putproperty "map 001 [3 3 6 3 6 3 6 3 6 3 6 3 6 3 6 3 6 3 3]
putproperty "map 01 [3 3 6 3 6 3 3]
putproperty "map 00 [27]
putproperty "map 10 [9 9 9]
putproperty "map 11 [3 3 3 9 3 3 3]
putproperty "map 1 [3 3 3]
putproperty "map 0 [9]
end
# if the 3-basis writing is [1 0 1] --> output 101
# if the 3-basis writing is [1 0 2] --> output 100
# Element from the list are translated into a word.
# 2 are replaced by 0
to evalue :list :mot
if emptyp :list [output :mot]
[
localmake "first first :list
if :first=2 [localmake "first 0]
localmake "mot word :mot :first
output evalue butfirst :list :mot
]
end
# Draws the block of rectangular alternanting
to des :list
localmake "somme 0
for (list "i 1 count :list) [
localmake "element item :i :list
localmake "somme :element+:somme
if even? :i [penup forward :element*:unit pendown ]
[rec :element*:unit :unit forward :element*:unit]
]
penup back :somme * :unit pendown
end
# Draws the carpet order :p
to tapis :p
clearscreen 3d hideturtle initmap
globalmake "compteur 0
carpet 810 :p
write "nombre\ de\ polygones:\ print :compteur
view3d
end
# Is this number even?
to even? :i
output 0=modulo :i 2
end
# Remove the last 1 from :list
to deletelastone :list
for (list "i count :list 1 minus 1) [
localmake "element item :i :list
if :element=1 [localmake "list replace :list :i 0 stop] [if :element=2 [stop]]
]
output :list
end
# Draws the Serpinski carpet
# along axis (ox), (oy) and (oz)
to draw3carpet :size :order :z
penup home
uppitch 90 forward (:z-1)*:unite downpitch 90 pendown
setpencolor blue run :order :size
penup home
leftroll 90 forward (:z-1)*:unite downpitch 90 pendown
setpencolor yellow run :order :size
penup home
uppitch 90 forward :size right 90 forward (:z-1)*:unite downpitch 90 pendown
setpencolor magenta run :order :size
end
# Menger’s sponge order :p and size :size
to menger :size :p
globalmake "unite :size/(power 3 :p)
for (list "z 1 power 3 :p) [
localmake "cantorz cantor :z :p []
localmake "last last :cantorz
localmake "cantorz butlast :cantorz
if :last=0 [localmake "order evalue deletelastone :cantorz "]
[localmake "order evalue :cantorz "]
localmake "order word "coupe :order
draw3carpet :size :order :z
penup uppitch 90 forward :unit downpitch 90 pendown
]
draw3carpet :size :order (power 3 :p)+1
end
# Main procedure
# Draws a sponge order :p with side length 405
to sponge :p
clearscreen setsc 0 3d hideturtle
localmake "time pasttime
initmap
globalmake "counter 0
if :p=0 [cube 405] [menger 405 :p]
# Displays the time to build the sponge
write "Polygons\ number:\ print :counter
write "Time:\ print pasttime -:time
view3d
end
# Different sections for menger order 2
to coupe1 :size
repeat 4 [carpet :size/3 1 penup forward :size right 90 pendown]
end
to coupe0 :size
carpet :size 2
end
# Different sections for Menger order 3
to coupe10 :size
repeat 4 [carpet :size/3 2 penup forward :size right 90 pendown]
end
to coupe01 :size
repeat 4 [repeat 2 [coupe1 :size/3 penup forward :size/3 pendown] forward :size/3 right 90]
end
to coupe11 :size
repeat 4 [coupe1 :size/3 penup forward :size right 90 pendown]
end
to coupe00 :size
carpet :size 3
end
# Different sections for Menger order 4
to coupe000 :size
carpet :size 4
end
to coupe100 :size
repeat 4 [carpet :size/3 3 penup forward :size right 90 pendown]
end
to coupe010 :size
repeat 4 [repeat 2 [coupe10 :size/3 penup forward :size/3 pendown] forward :size/3 right 90]
end
to coupe001 :size
repeat 4 [repeat 2 [coupe01 :size/3 penup forward :size/3 pendown] forward :size/3 right 90]
end
to coupe110 :size
repeat 4 [coupe10 :size/3 penup forward :size pendown right 90 ]
end
to coupe111 :size
repeat 4 [coupe11 :size/3 penup forward :size right 90 pendown]
end
to coupe101 :size
repeat 4 [coupe01 :size/3 penup forward :size right 90 pendown]
end
to coupe011 :size
repeat 4 [repeat 2 [coupe11 :size/3 penup forward :size/3 pendown] forward :size/3 right 90]
end
to coupe :size
carpet :size 1
end
to cube :size
repeat 2 [
setpencolor blue rec :size :size penup forward :size downpitch 90 pendown
setpencolor yellow rec :size :size penup forward :size downpitch 90 pendown
]
setpencolor magenta
penup leftroll 90 left 90 forward :size right 90 pendown rec :size :size
penup right 90 forward :size left 90 rightroll 90 right 90 forward :size left 90 rightroll 90 pendown rec :size :size
leftroll 90 left 90 forward :size right 90
end
Then, we set memory allocated to XLOGO to 640 Mb: sponge 4