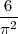 ≈ 0,6079. To exhibit this result, we’re going to:
≈ 0,6079. To exhibit this result, we’re going to:
In fact, a famous result in numbers theory says that the probability for two randomly chosen integers to be coprime
is 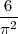 ≈ 0,6079. To exhibit this result, we’re going to:
≈ 0,6079. To exhibit this result, we’re going to:
In a similar way as the precevious note, notice the parenthesis around gcd random 1000000 random 1000000.
Otherwise, the interpreter will try to evaluate 1 000 000 = 1. You can write in other way: if 1=gcd random
1000000 random 1000000
We execute the program test.
We obtain some values close to the theorical probability: 0,6097. This frequency is an approximation of
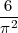 .
.
Thus, if I note f the frequency, we have: f ≈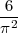
Hence, π2 ≈ and π ≈
and π ≈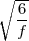 .
.
I append to my program a line that gives this π approximation in procedure test:
Now, we modify the program because I want to set the number of tries. I want to try with 10 000 and perhaps more tries.
Quite interesting, isn’t it?