Le programme précédent a pour principal avantage d’exploiter la structure naturellement récursive du solide
fractal. On peut noter que cette même méthode peut être réemployer pour générer d’autres solides fractals,
ou plus simplement, d’autres courbes fractales. En tout cas, La conséquence immédiate de l’approche
récursive est un code court et simple à comprendre. Malheureusement, on s’aperçoit qu’une éponge
d’ordre 3 nécessite déjà 48 000 polygônes. Il faut alors régler la mémoire allouée à XLogo à
256 Mo dans le panneau des préférences pour que le programme puisse s’exécuter entièrement.
Si l’on souhaite tracer une éponge de Menger d’ordre 4, on va vite être bloqué par un dépassement mémoire.
Nous allons voir dans cette partie un programme basé sur un algorithme complètement différent, il permettra de
créer une éponge de Menger d’ordre 0,1,2,3 ou 4.
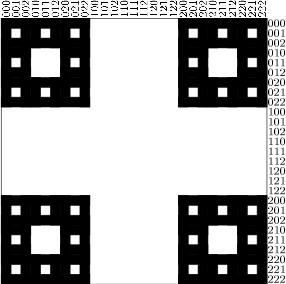
L’éponge de Menger est en fait la généralisation en 3 dimensions d’une figure du
plan appelée le tapis de Sierpinski. Voici les premières itérations de cette figure :
 Etape 0
Etape 0 |
 Etape 1
Etape 1 |
 Etape 2
Etape 2 |
 Etape 3
Etape 3 |
Le motif présent sur chacune des faces d’une éponge de Menger d’ordre p est un tapis de Sierpinski d’ordre
p.
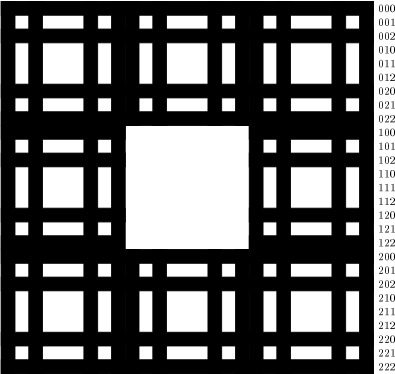
L’objectif est déjà de réussir à minimiser le
nombre de polygônes nécessaires pour dessiner un tapis de Sierpinski. L’exemple suivant explique le
procédé employé pour créer un tapis de Sierpinski d’ordre 3. Ici, le carré initial comporte donc
33 = 27 lignes et 27 colonnes. On écrit en base 3 le numéro de chacune des lignes et de chacune des
colonnes.
- Première étape : Pour toutes les lignes dont le numéro ne comporte aucun 1, on trace une ligne de 27
carreaux. Par symétrie, on effectue la même opération sur les colonnes.
- Deuxième étape : On s’intéresse à présent aux lignes dont le numéro comporte un seul 1 en
première position. On trace successivement par alternance des rectangles de longueur 9 carreaux. On reporte
alors cette opération sur les colonnes par symétrie .
- Troisième étape : On s’intéresse à présent aux lignes dont le numéro comporte un seul 1 en
deuxième position. On trace successivement par alternance des rectangles en suivant le schéma
[3 3 6 3 6 3 3]. (3 carreaux tracés, 3 non tracés, 6 tracés etc...) On reporte alors par symétrie cette
opération sur les colonnes.
- Dernière étape : On s’intéresse alors aux lignes dont le numéro comporte deux 1 placés aux
premières positions. On trace successivement par alternance des rectangles en suivant le schéma
[3 3 3 9 3 3 3]. On reporte ensuite cette opération sur les colonnes.
La construction du tapis de Sierpinski d’ordre 3 est alors terminée. Pour créer ce tapis, il a fallu utiliser en tout :
16 + 16 + 32 + 16 = 80 polygones.
Pour récapituler la construction précédente, voici les
différents types de schémas de colonnes suivant leur numéro de lignes. (Le symbole * désigne le chiffre 0 ou le
chiffre 2)
| Numéro de ligne du type | Schéma à appliquer |
| *** | 27 |
| 1** | 9 9 9 |
| *1* | 3 3 6 3 6 3 3 |
| 11* | 3 3 3 9 3 3 3 |
|
Sur le même principe, pour créer un tapis d’ordre 4, on utilisera un carré avec 34 = 81 carreaux. Les numéros
de ligne et de colonne possèderont donc 4 chiffres dans leur décomposition en base 3. Pour chaque type de
numéro de lignes, voici le schéma à appliquer (le symbole * désigne le chiffre 0 ou le chiffre 2) :
| Numéro de ligne du type | Schéma à appliquer |
| **** | 81 |
| 1*** | 27 27 27 |
| *1** | 9 9 18 9 18 9 9 |
| **1* | 3 3 6 3 6 3 6 3 6 3 6 3 6 3 6 3 6 3 3 |
| *11* | 3 3 3 9 3 3 6 3 3 9 3 3 6 3 3 9 3 3 3 |
| 1*1* | 3 3 6 3 6 3 3 27 3 3 6 3 6 3 3 |
| 11** | 9 9 9 27 9 9 9 |
| 111* | 3 3 3 9 3 3 3 27 3 3 3 9 3 3 3 |
496 polygônes sont alors nécessaires pour tracer un tapis de Sierpinski d’ordre 4.
|
Enfin, voici les chémas de constructions de colonnes pour les solides d’ordre 2 :
| Numéro de ligne du type | Schéma à appliquer |
| ** | 9 |
| 1* | 3 3 3 |
|
#trace un tapis de Sierpinski d’ordre :p et de taille :size
pour carpet :size :p
donne "unit :size/(puissance 3 :p)
si :p=0 [ rec :size :size stop]
si :p=1 [repete 4 [rec :size :unit av :size td 90 ] stop]
repetepour (liste "x 1 puissance 3 :p) [
soit "cantorx cantor :x :p []
# On ne trace pas les éléments ayant un 1 en derniere position
si non (1=dernier :cantorx) [
soit "nom evalue saufdernier :cantorx "
drawColumn :x rprop "map :nom
]
]
fin
# Retourne la décomposition en base 3 du nombre x
# p indice de profondeur 3^p
# :list liste vide au démarrage
pour cantor :x :p :list
si :p=0 [retourne :list]
soit "a puissance 3 :p-1
si :x<= :a [
retourne cantor :x :p-1 phrase :list 0]
[ si :x<=2*:a [retourne cantor :x-:a :p-1 phrase :list 1]
retourne cantor :x-2*:a :p-1 phrase :list 0]
fin
# Trace la colonne numéro x en respectant le schéma de construction défini dans la liste
pour drawcolumn :x :list
lc td 90 av (:x-1)*:unit tg 90 bc des :list
lc tg 90 av (:x-1)*:unit td 90 av :x*:unit td 90 bc des :list
lc tg 90 re :x*:unit bc
fin
# Trace un rectangle de dimensions données
# Le polygone est enregistrées par le viewer3d
pour rec :lo :la
donne "compteur :compteur+1
polydef
repete 2 [av :lo td 90 av :la td 90]
polyfin
fin
# Initialise les différentes colonnes possibles pour les tapis d’ordre 1 à 4
pour initmap
dprop "map 111 [3 3 3 9 3 3 3 27 3 3 3 9 3 3 3]
dprop "map 110 [9 9 9 27 9 9 9]
dprop "map 101 [3 3 6 3 6 3 3 27 3 3 6 3 6 3 3]
dprop "map 011 [3 3 3 9 3 3 6 3 3 9 3 3 6 3 3 9 3 3 3]
dprop "map 000 [81]
dprop "map 100 [27 27 27]
dprop "map 010 [9 9 18 9 18 9 9]
dprop "map 001 [3 3 6 3 6 3 6 3 6 3 6 3 6 3 6 3 6 3 3]
dprop "map 01 [3 3 6 3 6 3 3]
dprop "map 00 [27]
dprop "map 10 [9 9 9]
dprop "map 11 [3 3 3 9 3 3 3]
dprop "map 1 [3 3 3]
dprop "map 0 [9]
fin
# Si la decomposition est [1 0 1] --> retourne 101
pour evalue :list :mot
si vide? :list [retourne :mot]
[
soit "mot mot :mot premier :list
retourne evalue saufpremier :list :mot
]
fin
# Trace les blocs de rectangles de chaque colonne par alternance
pour des :list
soit "somme 0
repetepour (liste "i 1 compte :list) [
soit "element item :i :list
soit "somme :element+:somme
si pair? :i [lc av :element*:unit bc ] [rec :element*:unit :unit av :element*:unit]
]
lc re :somme * :unit bc
fin
# Teste si un nombre est pair
pour pair? :i
retourne 0=reste :i 2
fin
pour tapis :p
ve perspective ct initMap
donne "compteur 0
carpet 810 :p
tape "Nombre\ de\ polygones:\ ec :compteur
vue3d
fin
|
tapis 3 dessine un tapis de Sierpinski d’ordre 3 de côté 810. Voilà, nous sommes prêts à passer à
l’éponge de Menger!
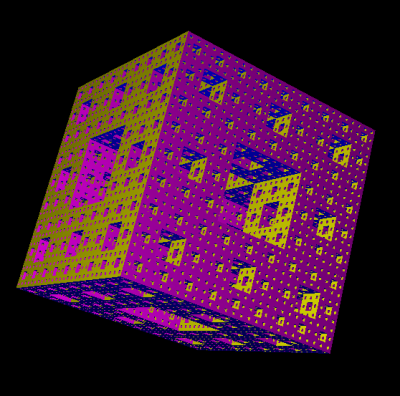
L’éponge de Menger possède de multiples propriétés de symétrie.
Pour la générer nous allons tracer les différentes sections suivant le plan (xOy) puis reporter ces figures
suivant (yOz) et (xOz). Pour bien expliquer ce qui se passe, restons sur l’exemple de l’éponge d’ordre
3 :
Lorsque l’on coupe l’éponge par un plan vertical, on peut obtenir quatre motifs différents :
Pour tracer une éponge d’ordre 3, nous allons parcourir les nombres de 1 à 27, c’est à dire de 001 à 222 en base
3. Pour chaque numéro, on appliquera la section adéquate que l’on reportera suivant les 3 directions (Ox), (Oy)
et (Oz).
Le programme suivant permet de tracer les solides de Menger d’ordre 0,1,2,3,4. Le nombre de
procédures est important donc j’apporterai quelques éclaircissements ensuite.
#trace un tapis de Sierpinski d’ordre :p et de taille :size
pour carpet :size :p
donne "unit :size/(puissance 3 :p)
si :p=0 [ rec :size :size stop]
si :p=1 [repete 4 [rec :size :unit av :size td 90 ] stop]
repetepour (liste "x 1 puissance 3 :p) [
soit "cantorx cantor :x :p []
# On ne trace pas les éléments ayant un 1 en derniere position
si non (1=dernier :cantorx) [
soit "nom evalue saufdernier :cantorx "
drawColumn :x rprop "map :nom
]
]
fin
# Retourne la décomposition en base 3 du nombre x
# p indice de profondeur 3^p
# :list liste vide au démarrage
pour cantor :x :p :list
si :p=0 [retourne :list]
soit "a puissance 3 :p-1
si :x<= :a [
retourne cantor :x :p-1 phrase :list 0]
[ si :x<=2*:a [retourne cantor :x-:a :p-1 phrase :list 1]
retourne cantor :x-2*:a :p-1 phrase :list 2]
fin
# Trace la colonne number x en respectant le schéma de construction défini dans la liste
pour drawcolumn :x :list
lc td 90 av (:x-1)*:unit tg 90 bc des :list
lc tg 90 av (:x-1)*:unit td 90 av :x*:unit td 90 bc des :list
lc tg 90 re :x*:unit bc
fin
# Trace un rectangle de dimensions données
# Le polygone est enregistrées par le viewer3d
pour rec :lo :la
donne "compteur :compteur+1
polydef
repete 2 [av :lo td 90 av :la td 90]
polyfin
fin
# Initialise les différentes colonnes possibles pour les tapis d’ordre 1 à 4
pour initmap
dprop "map 111 [3 3 3 9 3 3 3 27 3 3 3 9 3 3 3]
dprop "map 110 [9 9 9 27 9 9 9]
dprop "map 101 [3 3 6 3 6 3 3 27 3 3 6 3 6 3 3]
dprop "map 011 [3 3 3 9 3 3 6 3 3 9 3 3 6 3 3 9 3 3 3]
dprop "map 000 [81]
dprop "map 100 [27 27 27]
dprop "map 010 [9 9 18 9 18 9 9]
dprop "map 001 [3 3 6 3 6 3 6 3 6 3 6 3 6 3 6 3 6 3 3]
dprop "map 01 [3 3 6 3 6 3 3]
dprop "map 00 [27]
dprop "map 10 [9 9 9]
dprop "map 11 [3 3 3 9 3 3 3]
dprop "map 1 [3 3 3]
dprop "map 0 [9]
fin
# Si la decomposition est [1 0 1] --> retourne 101
# Si la decomposition est [1 0 2] --> retourne 100
# Les éléments de la liste sont concaténés en un mot.
# De plus, es 2 sont remplacés par des zéros
pour evalue :list :mot
si vide? :list [retourne :mot]
[
soit "first premier :list
si :first=2 [soit "first 0]
soit "mot mot :mot :first
retourne evalue saufpremier :list :mot
]
fin
# Trace les blocs de rectangles de chaque colonne par alternance
pour des :list
soit "somme 0
repetepour (liste "i 1 compte :list) [
soit "element item :i :list
soit "somme :element+:somme
si pair? :i [lc av :element*:unit bc ] [rec :element*:unit :unit av :element*:unit]
]
lc re :somme * :unit bc
fin
# Teste si un nombre est pair
pour pair? :i
retourne 0=reste :i 2
fin
pour tapis :p
ve perspective ct initMap
donne "compteur 0
carpet 810 :p
tape "Nombre\ de\ polygones:\ ec :compteur
vue3d
fin
# Supprime le dernier 1 dans la liste :list
pour deletelastone :list
repetepour (liste "i compte :list 1 moins 1) [
soit "element item :i :list
si :element=1 [soit "list remplace :list :i 0 stop] [si :element=2 [stop]]
]
retourne :list
fin
# Eponge de Menger de taille donnée et de profondeur :p
pour menger :size :p
donne "unite :size/(puissance 3 :p)
repetepour (liste "z 1 puissance 3 :p) [
soit "cantorz cantor :z :p []
soit "last dernier :cantorz
soit "cantorz saufdernier :cantorz
si :last=0 [soit "order evalue deleteLastOne :cantorz "] [soit "order evalue :cantorz "]
soit "order mot "coupe :order
draw3carpet :size :order :z
lc cabre 90 av :unit pique 90 bc
]
draw3carpet :size :order (puissance 3 :p)+1
fin
# Trace les tapis de Sierpinski d’ordre :p
# suivant chaque axe (Ox), (Oy) et (Oz)
# à l’altitude :z
pour draw3carpet :size :order :z
lc origine
cabre 90 av (:z-1)*:unite pique 90 bc
fcc bleu exec :order :size
lc origine
rg 90 av (:z-1)*:unite pique 90 bc
fcc jaune exec :order :size
lc origine
cabre 90 av :size td 90 av (:z-1)*:unite pique 90 bc
fcc magenta exec :order :size
fin
# Procédure principale
# Trace une eponge de Menger de profondeur p
pour eponge :p
ve perspective ct
soit "temps temps
initMap
donne "compteur 0
si :p=0 [cube 405] [menger 405 :p]
# Affiche le temps mis et le nombre de polygone nécessaire à la construction
tape "Nombre\ de\ polygones:\ ec :compteur
tape "Temps\ mis:\ ec temps -:temps
vue3d
fin
# Section pour le Menger d’ordre 2
pour coupe1 :size
repete 4 [carpet :size/3 1 lc av :size td 90 bc]
fin
pour coupe0 :size
carpet :size 2
fin
# Section pour le Menger d’ordre 3
pour coupe10 :size
repete 4 [carpet :size/3 2 lc av :size td 90 bc]
fin
pour coupe01 :size
repete 4 [repete 2 [coupe1 :size/3 lc av :size/3 bc] av :size/3 td 90]
fin
pour coupe11 :size
repete 4 [coupe1 :size/3 lc av :size td 90 bc]
fin
pour coupe00 :size
carpet :size 3
fin
# Section pour le Menger d’ordre 4
pour coupe000 :size
carpet :size 4
fin
pour coupe100 :size
repete 4 [carpet :size/3 3 lc av :size td 90 bc]
fin
pour coupe010 :size
repete 4 [repete 2 [coupe10 :size/3 lc av :size/3 bc] av :size/3 td 90]
fin
pour coupe001 :size
repete 4 [repete 2 [coupe01 :size/3 lc av :size/3 bc] av :size/3 td 90]
fin
pour coupe110 :size
repete 4 [coupe10 :size/3 lc av :size bc td 90 ]
fin
pour coupe111 :size
repete 4 [coupe11 :size/3 lc av :size td 90 bc]
fin
pour coupe101 :size
repete 4 [coupe01 :size/3 lc av :size td 90 bc]
fin
pour coupe011 :size
repete 4 [repete 2 [coupe11 :size/3 lc av :size/3 bc] av :size/3 td 90]
fin
pour coupe :size
carpet :size 1
fin
pour cube :size
repete 2 [
fcc bleu rec :size :size lc av :size pique 90 bc
fcc jaune rec :size :size lc av :size pique 90 bc
]
fcc magenta
lc rg 90 tg 90 av :size td 90 bc rec :size :size
lc td 90 av :size tg 90 rd 90 td 90 av :size tg 90 rd 90 bc rec :size :size
rg 90 tg 90 av :size td 90
fin
pour cubes
ve perspective ct
soit "temps temps
initMap
donne "compteur 0
repete 4 [si compteur=1 [cube 405] [menger 405 compteur-1] lc av 1000 td 90 bc ]
# Affiche le temps mis et le nombre de polygone nécessaire à la construction
tape "Nombre\ de\ polygones:\ ec :compteur
tape "Temps\ mis:\ ec temps -:temps
vue3d
fin
|
Ensuite, on règle la mémoire allouée à XLOGO à 640 Mo : eponge 4